NeurIPS, also known as the Conference on Neural Information Processing Systems, is one of the top-tier annual machine learning conferences, along with ICML and ICLR. The most recent conference, held in New Orleans, attracted over 16,000 participants, with 3,500 papers accepted.
Two Sigma strives to remain at the cutting edge of machine learning research, valuing the opportunities to learn from and exchange ideas with peers in the field–even when those ideas don’t pertain directly to our daily work. As we have done since 2014, Two Sigma sponsored the NeurIPS 2023 conference, and numerous employees attended.
In this article, the authors spotlight a (far from exhaustive) selection of the most innovative, relevant, and captivating papers and presentations from the event. Unsurprisingly, given the rate at which large language models (LLMs) are advancing, they garnered a great deal of attention at the 2023 event.
Outstanding Paper Award : Are Emergent Abilities of Large Language Models a Mirage? [Oral]
The authors question some of the mystique surrounding LLMs, in particular the claim that they possess emergent abilities or, as another group of researchers has defined it, “abilities that are not present in smaller-scale models but are present in large-scale models; thus they cannot be predicted by simply extrapolating the performance improvements on smaller-scale models”
The authors hypothesize that nonlinear or discontinuous metrics are often at root responsible for earlier reported seemingly emergent abilities. The authors’ theory presents three factors that explain some of these sharp and unpredictable changes that occur with increasing model scale.
- Metrics that nonlinearly or discontinuously scale with the per-token error rate
- Insufficient resolution to evaluate model performance in a smaller parameters space, which can be remedied with increased testing data
- Insufficient sampling
The authors’ contributions include testing and confirming their hypothesis using GPT-3 and InstructGPT; demonstrating that emergent abilities appear only for specific metrics and not for model families on a given task; and inducing new, seemingly emergent abilities, by varying evaluation metric.
Figure 1. demonstrates the claimed emergent abilities of various model families.
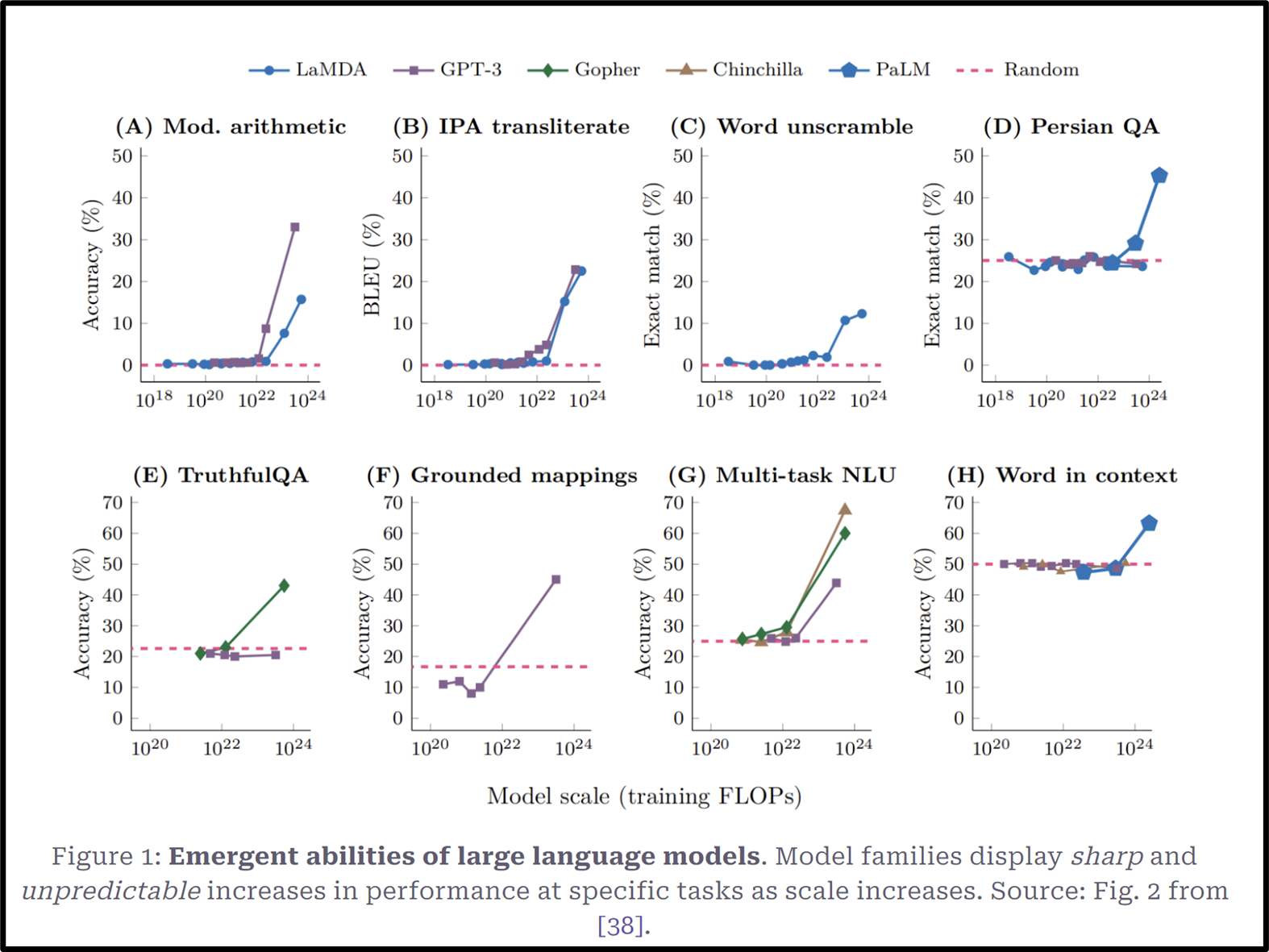
Figure 3. demonstrates that claimed emergent abilities for arithmetic operations disappear in the GPT-3 model family when changing from a non-linear metric, such as accuracy, to a linear metric, such as token edit distance. With a different metric performance scales linearly with model parameter size.
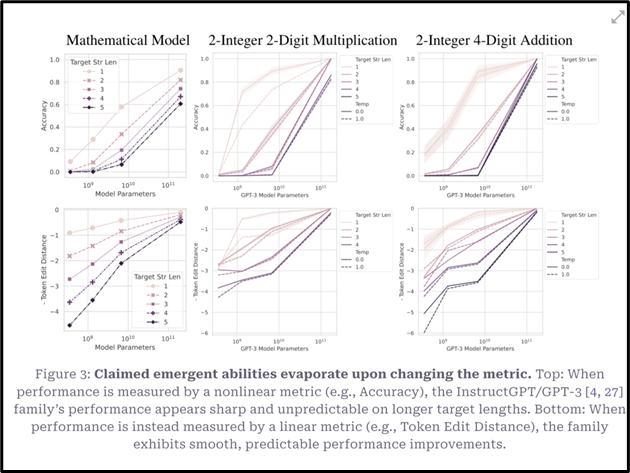
Figure 4. demonstrates that even on a non-linear metric such as Accuracy, performance scales continuously when additional test data is included, increasing resolution, for the same arithmetic task.
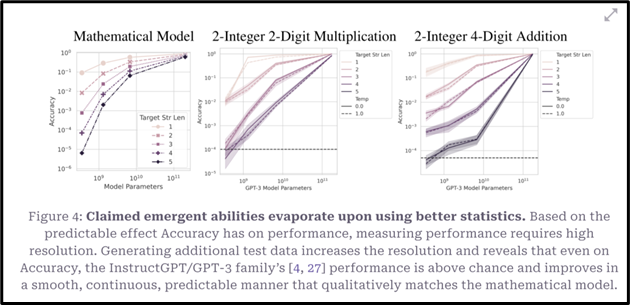
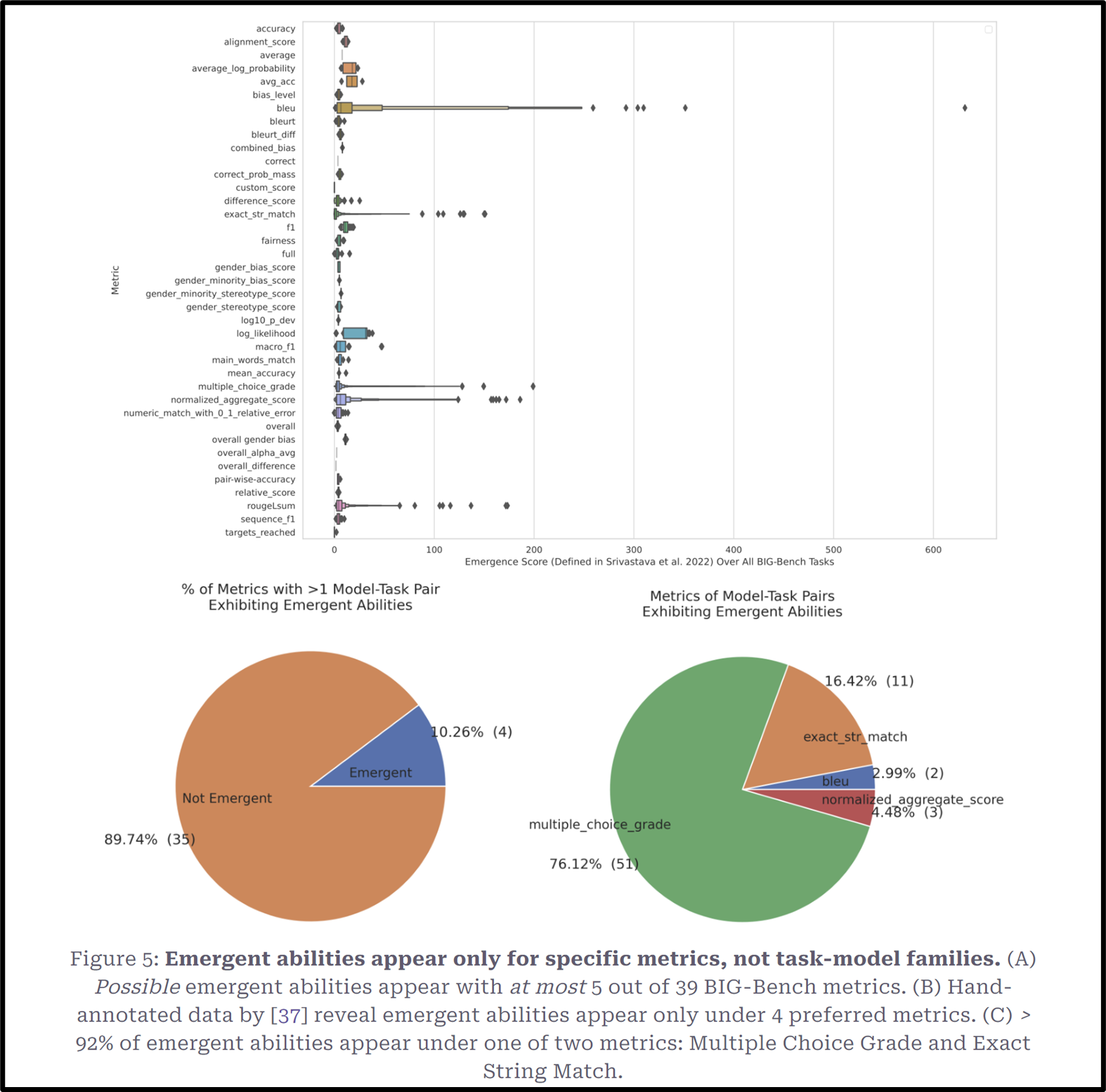
Figure 5. highlights that emergent abilities occur for only a small subset of the BIG-Bench metrics such as bleu score, Multiple Choice Grade, and Exact String Match. These abilities are tied to specific metrics and NOT task-model families.
This alternate explanation of emergent abilities suggests that they are not a fundamental property of the LLM model family or task. The work presents a cautionary note for all modelers and technicians: the choice of metric, the appropriate scale of test data and proper controls are crucial for forecasts results from a model.
QLoRA: Efficient Finetuning of Quantized LLMs [Oral]
LLMs hold tremendous promise to improve performance on bespoke tasks via tailored customization. However such functionality has often been inaccessible, due to large compute requirements. QLoRA (Quantized Low Rank Adapters) adds to the suite of Parameter Efficient Fine-tuning [PEFT] solutions for fine-tuning LLMs by minimizing memory requirements without sacrificing performance. In fact, with QLoRA a 65B parameter model can be fine-tuned on a single 48GB GPU, with state-of-the-art results on small, high-quality datasets.
Memory requirements significantly reduced with QLora.

Fine-tuning to customize a 70B LLM model is expensive. PEFT techniques, such as LoRA, have been shown to reduce computational requirements.
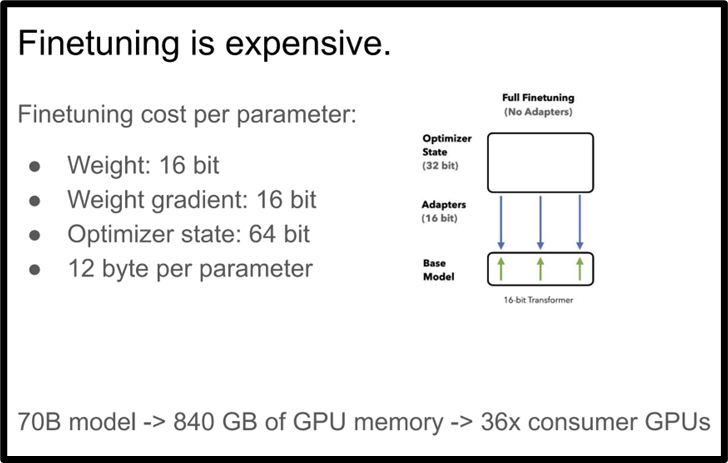

Using 4-bit Quantization on a frozen base model with LoRA further reduced memory requirements.
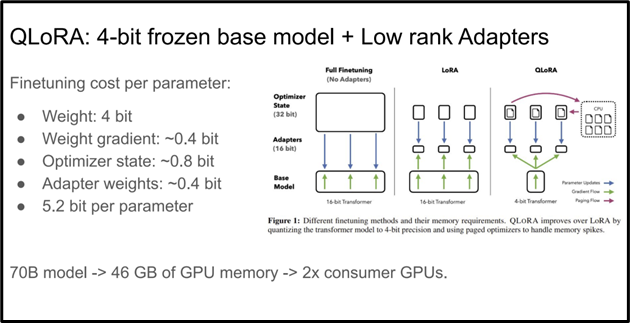
The authors’ best model family fine-tuned with QLora, named Guanaco, boasts reaching 99.3% of ChatGPT performance while requiring only 24 hours of training on a single CPU. This innovation was made possible by a 4-bit NormalFloat data type that has normally distributed weights, double quantization to reduce the average memory footprint, and paged optimization to mitigate memory spikes.
The implication of this work is further democratized access to LLM model customization, both in terms of speed and compute resources.
Outstanding Paper Runner-Up: Scaling Data-Constrained Language Models [Oral]
LLMs have trended recently towards ever-increasing dataset sizes and parameter counts. The authors of this paper have examined scaling of language models when data is constrained and propose a scaling law for compute optimality. Results include:
- Given a fixed computer budget, training with up to 4 epochs of repeated data is equivalent to using unique data
- The value of adding additional compute falls to zero with more data repetition
- Given scarce data, scaling may be mitigated by augmenting the training dataset with code data
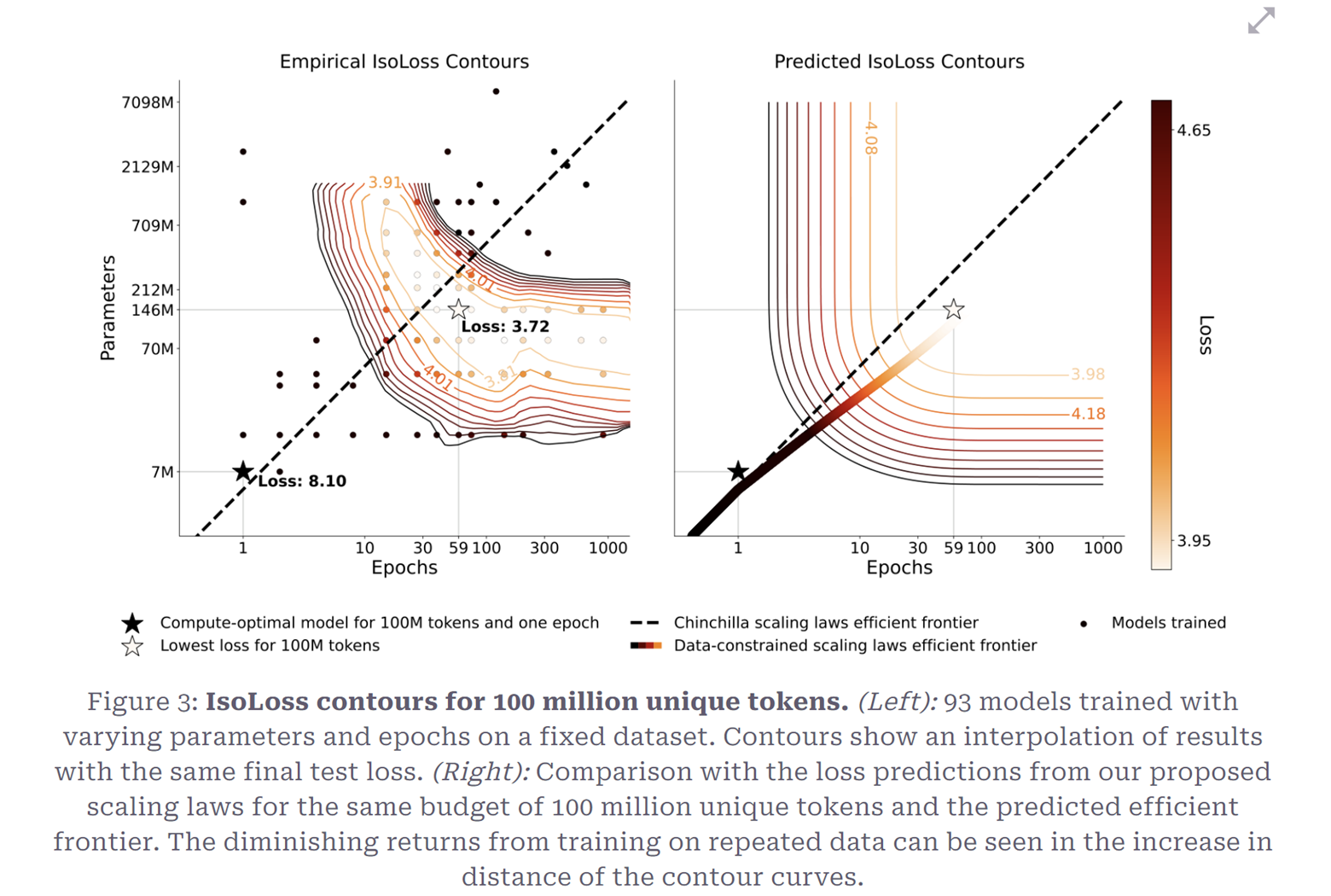
Direct Preference Optimization: Your Language Model is Secretly a Reward Model
Reinforcement learning from human feedback (RLHF) has been the default for language model alignment and incorporation of human preferences into LLMs responses. However, RLHF is both complex and computationally expensive. The procedure involves fitting a reward model of human preferences and then fine-tuning an unsupervised LLM via reinforcement learning that optimizes the reward, while ensuring that the LLM response is not divergent from the original model.
As an alternative, this paper’s authors offer Direct Preference Optimization (DPO) a stable, lightweight algorithm that condenses the constrained reward maximization problem of RLHF into the equivalent of a human preference classification problem.

DPO claims equivalent or better performance as compared to other algorithms in a streamlined and simplified format, reducing the barrier to generative model customization.
Modeling and Exploiting Data Heterogeneity Under Distribution Shifts
Most machine learning models exhibit degraded performance when evaluated on data that is different from that which they were trained on. A NeurIPS tutorial summarized what is currently known about such data “distribution shifts” and how models react to them.
In some cases, the relationship between the “in-distribution” performance and “out-of-distribution” performance can be a clean linear relationship, termed Accuracy on the Line. For example, vision models trained on the classic ImageNet dataset do worse when evaluated on ImageNetV2 than their native V1 ImageNet, but an improvement on one dataset generally corresponds directly to an improvement on the other. In the plots below, one can observe performance correspondences that are linear but below the y=x line.
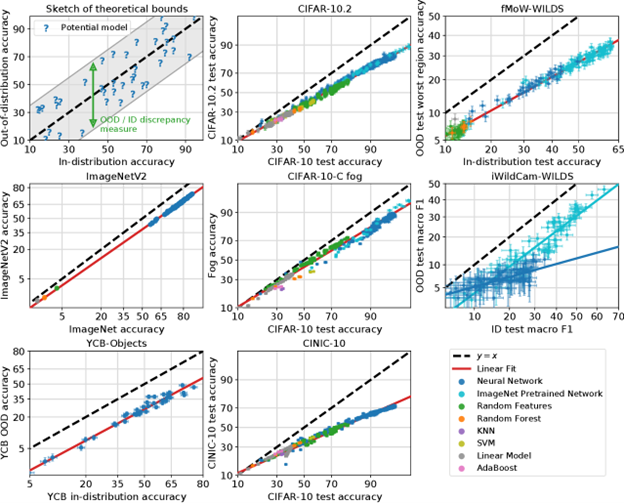
However, this clean relationship generally doesn’t hold when there are hidden confounding variables. The tutorial presenters proposed the following terminology to elaborate on this: X-shifts are changes in the marginal distribution of the covariates, and Y|X shifts are changes in the relationship between the outcome and the covariate.
For example, one US state in a demographic dataset might have a different distribution of ages from another state in that same dataset, and changing the distribution of ages on its own would be an X-shift. However, something else that changes between US states and influences observed phenomena yet is unobserved in the data (e.g., the climate or the economy)—that would be a Y|X shift.
The presenters claimed that Y|X shifts are not common in computer vision or natural language tasks, as the input data usually contains sufficient information to make a clear output determination. Such hidden data problems can be quite common in domains such as the social sciences, however. The Accuracy on the Line phenomenon is often not present when there are strong Y|X shifts, so what seem like model improvements on training data may not generalize to new data. Just adding more training data of the same type won’t solve the problem, as it will continue to lack the required variables. Such “confounding” concerns are a mainstay of causal inference, and various papers and posters at this year’s NeurIPS attempted to integrate causal inference and machine learning.
Understanding why certain data distribution shifts cause more problems than others is of great practical significance, but the tutorial concluded that researchers still have many things to learn in this area.
Sharpness Minimization Algorithms Do Not Only Minimize Sharpness To Achieve Better Generalization
The paper investigates the mystery of why an overparameterized neural network can generalize. To better understand this phenomenon, the authors provide theoretical and empirical results for two-layer neural ReLU networks under three scenarios.
Definition
- Minimizer: assume $f_\theta$ is an overparameterized model, loss function is $L(\theta) := \frac{1}{n} \sum_{i=1}^n \ell(f_\theta(x_i), y_i)$. Then the minimizer refers to the set of $\theta$ such that $L(\theta) = 0$.
- Sharpness: The sharpness refers to Tr$(\nabla^2 L(\theta)$.
- Sharpness-Aware Minimization: Refers to a body of recent work that implicitly regularizes the sharpness of the training loss landscape, for example [see 1 and 2 in “Cited works”, below]].
Three Questions
To structure their investigation, the authors pose three central questions, examine the existing literature where applicable, and finally attempt to determine whether each is demonstrably true or false. The three questions are as follows:
1. Does the flatness of the minimizers always correlate with the generalization capability?
The answer to the question turns out to be false, the authors found. Theoretically, [3] construct very sharp networks with good generalization. Empirically, [4] find that sharpness may not have a strong correlation with test accuracy for a collection of modern architectures and settings, partly due to the same reason—there exist sharp models with good generalization.
2. Do all the flattest neural network minimizers generalize well?
The authors determined that this can be false, even for simple architectures like 2-layer ReLU networks. But simply removing the bias in the first layer turns the aforementioned negative result into a positive result.
3. Will sharpness minimization algorithm fail to generalize when there exist non-generalizing flattest minimizers?
The authors found this question to be false. The sharpness-minimization algorithms can still generalize well even when there exist non-generalizing flattest minimizers. The author provides evidence that in regime: a 2-layer ReLU MLP with a simplified LayerNorm (without mean subtraction and bias), although there exist flattest minimizers that do not generalize, the sharpness minimization algorithm still finds the generalizable flattest model empirically. In this scenario, the sharpness minimization algorithm relies on other unknown mechanisms beyond minimizing sharpness to find a generalizable model.
Cited works:
[1] Peter L Bartlett, Philip M Long, and Olivier Bousquet. The dynamics of sharpness-aware minimization: Bouncing across ravines and drifting towards wide minima.
[2] Sanjeev Arora, Zhiyuan Li, and Abhishek Panigrahi. Understanding gradient descent on edge of stability in deep learning.
[3] Laurent Dinh, Razvan Pascanu, Samy Bengio, and Yoshua Bengio. Sharp minima can generalize for deep nets.
[4] Maksym Andriushchenko, Francesco Croce, Maximilian Muller, Matthias Hein, and Nicolas Flammarion. A modern look at the relationship between sharpness and generalization.
Conclusions
By investigating why an overparameterized neural network can generalize, and by finding answers to the three questions posed above, the authors show that the sharpness minimization algorithms are, empirically, powerful tools for finding neural networks with good generalization ability, though the theory behind it is not what people conjecture about. More theoretical study is needed to understand this phenomenon.
A U-turn on Double Descent: Rethinking Parameter Counting in Statistical Learning
The authors of this paper study the double-descent phenomenon, a regime pertaining to the relationship between model complexity and prediction error, in which increasing the number of parameters in machine learning models causes the test error first to decrease, then to increase, and finally to decrease again. For example:
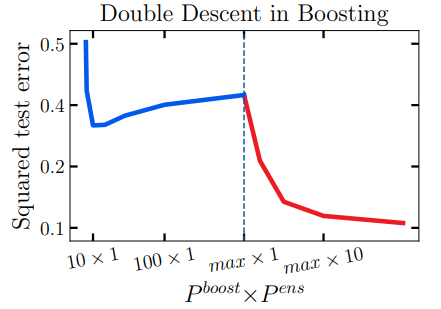
The authors investigate the double descent phenomenon in classical machine learning models, including linear regression, random forest, and boosting tree and “challenge the claim that observed cases of double descent truly extend the limits of a traditional U-shaped complexity-generalization curve therein.”
They propose to use a generalized effective number of parameters (similar to the degree of freedom in nonparametric models) to characterize the model complexity. The effective number of parameters will increase then decrease when adding more model parameters. Under this new metric, they find, the test error monotonically decreases.
Sampling from Gaussian Process Posteriors using Stochastic Gradient Descent
The authors of this paper propose a stochastic gradient algorithm as a computationally efficient method of approximately solving linear systems in Gaussian processes.
The algorithm first uses pathwise conditioning to write the posterior as a random function.
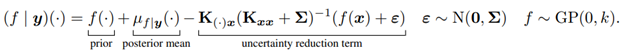
The authors use random Fourier features to approximate the prior:
![]()
Next, they use optimization-based representation for the posterior mean…
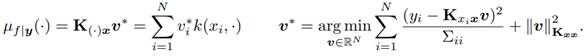
…and the SGD estimator for the mean:
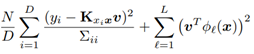
The algorithm also uses Nystrom approximation to further reduce the store and computation complexity:
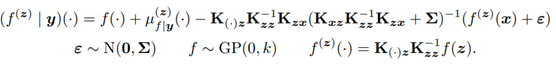
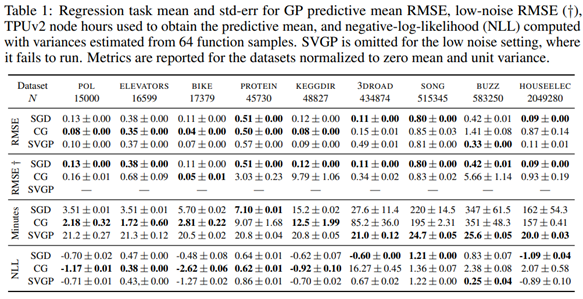
The authors then conduct experiments to empirically evaluate SGP GPs, to establish their predictive and decision-making characteristics. Ultimately, they find that SGD is competitive compared with conjugate gradient and SVGP.
DISCS: A Benchmark for Discrete Sampling
This paper’s authors perform a systematic comparison of existing discrete sampling algorithms and demonstrate the effectiveness of the recently proposed family of locally balanced samplers, which relies on the Langevin dynamics in discrete space.
The paper builds a benchmark with three tasks: sampling in classical graphical models, solving combinatorial optimization, and sampling from deep energy based models.
The benchmark provides APIs for custom sampling algorithms and custom target distributions to ease future research.






